[ Constrained 3D | Performance Analysis | Paraperspective | Dataset | Home ]

3D reconstruction of man-made scenes

The reconstructions below are obtained from a single image (a scanned postcard) in which some image points are identified (the white dots) and from geometric information, in the form of known planes,symmetries, known angles etc. From this information, the least-squares reconstructions are computed, together with estimates of the precision with which they are obtained.

In this work, the previous state-of-the-art, as of 2002, was improved by:


tour eiffel w/ some identified points tour eiffel reconstructed from one image

Eiffel Tower

The rightmost image shows the reconstruction with and without texture.
  • Number of points : 70.
  • Geometric information : 56 planarities and 45 known ratios of signed lengths that express the symmetry of the tower.
  • Estimated precision of reconstructed 3D points : 0.5%.
  • VRML model, short movie.

Folkemuseum w/ some identified points Folkemuseum from one image

Folkemuseum

The rightmost image shows the reconstruction.
  • Number of points : 131.
  • Geometric information : 75 planes and 26 known ratios of signed lengths.
  • Estimated precision of reconstructed 3D points : 1.5%.
  • VRML model, short movie.




More reconstructions

More information

PhD Abstract

We consider the problem of tridimensional reconstruction obtained from one or more images, when the 2D perspective projections of 3D points of interest are available, together with some geometric properties, such as planarities, alignments, symmetries, known angles between directions etc. Because these geometric properties occur mainly in man-made environments and objects, the presented method applies mostly to these cases.

  The method has two phases. In the first, the reconstruction problem is transformed into one of linear algebra, and the solutions to the initial problem are identified with that of the second. Thus, examining the dimension of the space of solutions allows to determine whether the provided information is sufficient to uniquely define a reconstruction.

  In the second phase, the maximum likelihood reconstruction is obtained. The reconstruction problem is transformed into a problem of unconstrained optimization by using a differential parameterization of the 3D points subject to geometric constraints.

  These two techniques combine into a reconstruction method that improves upon the current state-of-the-art by offering a great flexibility of use and by providing a reconstruction that is statistically characterized. The method is benchmarked using synthetic and real-world data.

Thesis supervisor :

Prof. José Santos Victor

Jury members :

Prof. Rachid Deriche Prof. Jorge Dias Prof. João Sentieiro
Prof. Mário Figueiredo Prof. José Santos Victor Prof. Pedro Aguiar


Performance analysis of uncalibrated reconstruction

It is known [MF92,F92,H93] that Euclidean 3D reconstruction is possible from three or more uncalibrated views. However, even though the solution to the reconstruction problem is indeed unique, this solution is extremely sensitive to noise in the input data. In probabilistic terms this is reflected by the fact that the covariance matrix of the maximum-likelihood estimator of 3D reconstuction has a high condition number and large diagonal elements.

Geometrically unconstrained uncalibrated 3D reconstruction
In this Image and Vision Computing article (a previous version of which appeared in BMVC '98), we show that a Gaussian error model is appropriate when the input consists of hand-identified image points and study the effect of noise amplitude, number and geometric disposition of cameras and number of 3D points on the precision of the obtained maximum-likelihood estimate. Also, we compare this precision with that of various maximum a-priori estimators that benefit from prior knowledge on some or all of the intrinsic camera calibration parameters. In conclusion, use more than three images. If possible, use a probabilistic a-priori on the intrinsic parameters. In all cases, check the covariance of your estimate (this assumes that your reconstruction is the result of maximizing a likelihood function, rather than an analytic solution), as neither known calibration nor high number of cameras and points garantee a good accuracy.
Comparison between geometrically constrained and unconstrained uncalibrated 3D reconstruction
In this BMVC'00 article, we show the effect of a-priori information about the geometry of the scene on the precision of the 3D reconstruction obtained from uncalibrated images. There have been many claims [BMV93,BB98] that the reconstruction is improved  when some geometric properties of the scene are known. However, we are not aware of quantitative studies of this question (dear reader, tell me if you are aware of such studies). The type of information considered is planarity and known angles between planes. In this work, we assume a Gaussian noise on the input and use the framework of maximum-likelihood and maximum a-priori estimation. In conclusion, known angles and planarities very effective at improving the precision , while knowing only planarities is much less effective.
References

Paraperspective reconstruction

Paraperspective reconstruction is a factorization-based method for 3D reconstruction. Factorization methods are simple to implement and mostly non-iterative methods. Because they use a parallel projection model, their accuracy with most real-world data -produced by perspective projection- is not great. However, the result of a factorization method constitutes a good starting position for an iterative perspective method and I have mostly used it as such.

  As its name implies, paraperspective reconstruction uses the more faithful paraperspective projection model instead of the orthographic projection model used in the original factorization method of Tomasi and Kanade [TK92]. Paraperspective reconstruction was first proposed by Poelman and Kanade [PK94] and this ICPR'00 article improves over the latter by presenting a truly closed-form method for paraperspective reconstruction.
Example reconstruction obtained with the proposed algorithm.
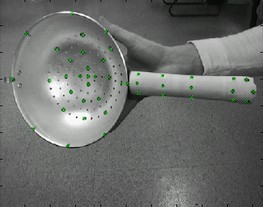
One out of 12 views of object
 other view of object (out of 12) reconstructed object and cameras Reconstructed object
Two out of twelve views of the object. Green crosses mark tracked points.
 Reconstructed object and (left) estimated camera positions. The geometric deformation is typical of paraperspective reconstruction at short-range.

References

Dataset


Here is a dataset consisting in six sequences. It has been used in the BMVC'98 and IVC'00 articles mentionned above.

  Each sequence has 5-10 images and the coordinates of some points that have been manually identified and tracked along the images. The least-squares reconstruction is included. The data is in Octave/Matlab format. Feel free to use it for testing your own reconstruction algorithms.

[ Constrained 3D | Performance Analysis | Paraperspective | Dataset | Home ]